LaTeX templates and examples — Assignments
Handy LaTeX templates for homework assignments to use at school, college, and university. They’re great for teachers to prep classes too.
Recent
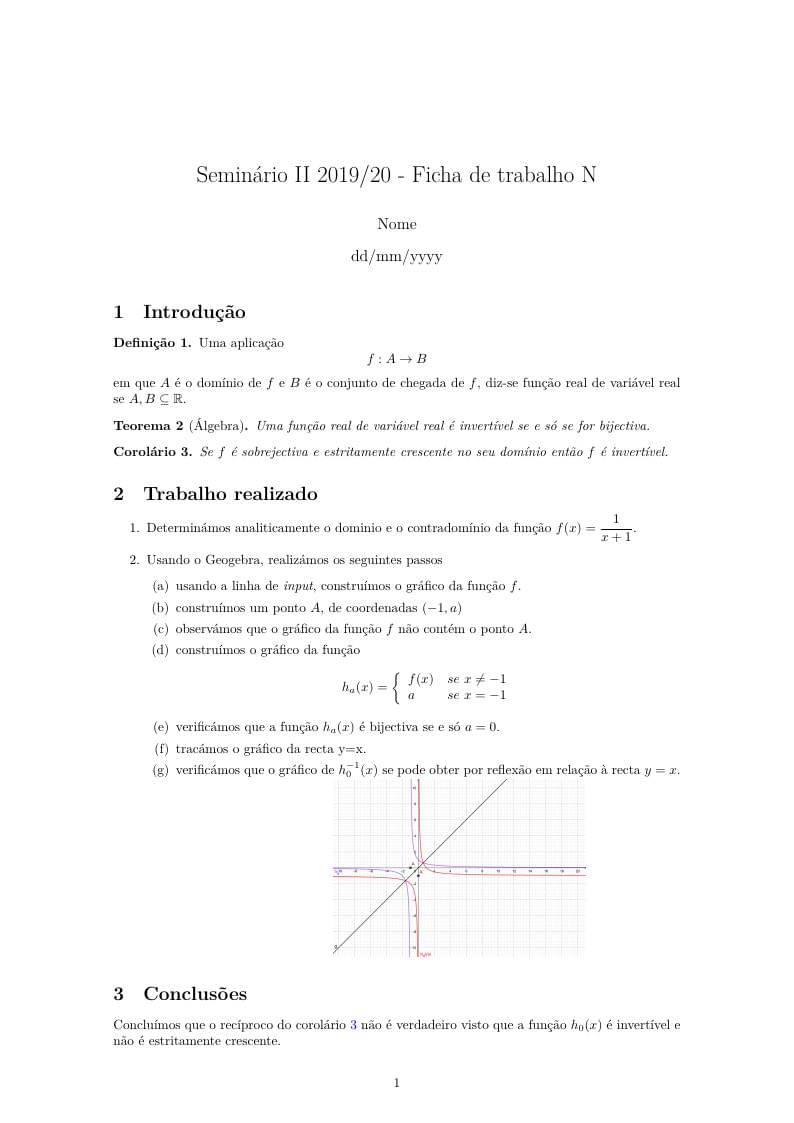
Ficheiro para registar os resultados das experiências realizadas na disciplina Seminário II - módulo funções em 2019/20

This LaTeX template was developed to create lists of exercises in the Information Systems and Systems Analysis and Development courses at Unichristus. This project is also on GitHub: https://github.com/profmauricioneto/template-list-unichristus

laborario 3 de calculo vectorial

A second project for Calculus 1 at Fitchburg State. Explore the proofs of some of the derivative rules and derive new rules from old.

This is the template for homework revised drafts for Dr. Sykes's Abstract Algebra class. It is adapted from Dana Ernst's original weekly homework template.

This is a template for Dordt College Math 304 students to use in preparing their proofs/solutions for submission to our class notes document.

Göteborg universitet / Chalmers

This LaTex file is composed using LaTex.It's my probability homework published here only with the purpose of making more people get to know and use LaTex well!

The path to success in this class is to do many problems. Unlike other courses, exclusively doing reading(s) will not help. Coming to lecture is akin to watching workout videos; thinking about and solving problems on your own is the actual ``working out''. Feel free to \qu{work out} with others; \textbf{I want you to work on this in groups.} Reading is still \textit{required}. But for this homework set, I can't find anything from the 7th edition of Ross except the first few pages of Chapter 4 that are \qu{worth it} for you to read. The problems below are color coded: \ingreen{green} problems are considered \textit{easy} and marked \qu{[easy]}; \inorange{yellow} problems are considered \textit{intermediate} and marked \qu{[harder]}, \inred{red} problems are considered \textit{difficult} and marked \qu{[difficult]}, \inpurple{purple} problems are extra credit. The \textit{easy} problems are intended to be ``giveaways'' if you went to class. Do as much as you can of the others; I expect you to at least attempt the \textit{difficult} problems. This homework is worth 100 points but the point distribution will not be determined until after the due date. Late homework will be penalized 10 points per day. Between 1--15 points are arbitrarily given as a bonus (conditional on quality) if the homework is typed using \LaTeX. Links to instaling \LaTeX~and program for compiling \LaTeX~is found on the syllabus. You are encouraged to use \url{overleaf.com} (make sure you upload both the hwxx.tex and the preamble.tex file). If you are handing in homework this way, read the comments in the code; there are two lines to comment out and you should replace my name with yours and write your section. If you are asked to make drawings, you can take a picture of your handwritten drawing and insert as a figure or leave space using the \qu{$\backslash$vspace} command and draw them in after printing or attach them stapled. The document is available with spaces for you to write your answers. If not using \LaTeX, print this document and write in your answers. \textbf{Handing it in without this printout is NO LONGER ACCEPTABLE.} Keep this page printed for your records. Write your name and section below where section A is if you're registered for the 9:15AM--10:30AM lecture and section B is if you're in the 12:15PM-1:30PM lecture.
\begin
Discover why over 25 million people worldwide trust Overleaf with their work.