Series de Fourier
Author:
Ramón
Last Updated:
10 years ago
License:
Creative Commons CC BY 4.0
Abstract:
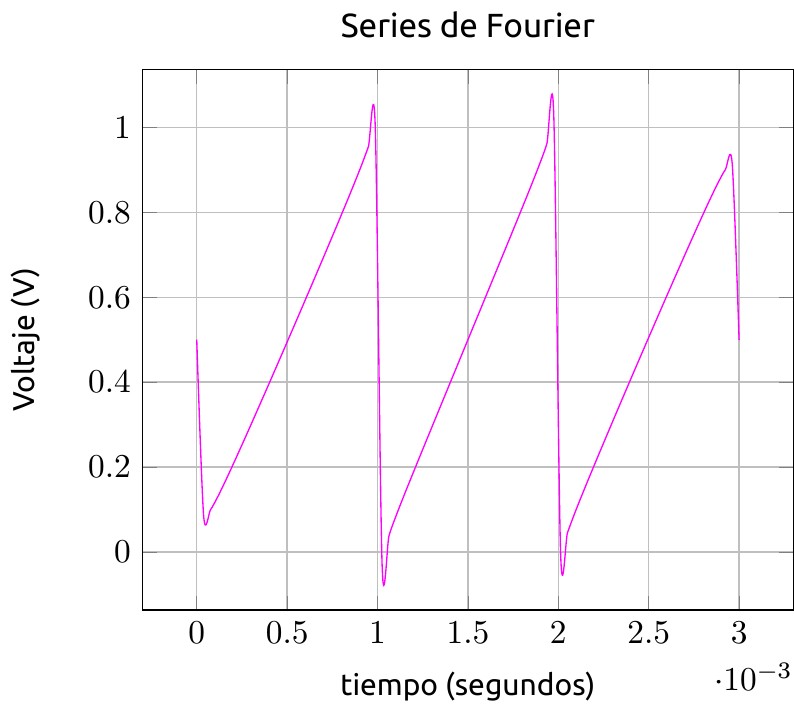
Este ejemplo demuestra como se puede sintetizar una señal periódica de "diente de sierra" partiendo de las Series de Fourier, utilizando sumas de funciones senoidales que van desde la que tiene la frecuencia fundamental de la señal hasta sus armónicas. Para ello se usa el paquete pgfplots y el comando \pgfplotsinvokeforeach{,...,} y luego se suma de forma acumulativa para formar la función \sumacurva, definida como una variable que parte del cero (0).

\begin
Discover why over 25 million people worldwide trust Overleaf with their work.